Taken from "Practical Astronomy With Your Calculator or Spreadsheet" 4th ed. by P. Duffett-Smith and J. Zwart.
The first calculator computes the day Easter falls in any given year after 1582. This was the year that Pope Gregory XIII implemented his improvements on the Julian calendar. [Specifically, he dropped 10 days in October 1582 from the calendar and decreed that century years are only leap years if divisible 400.] By careful management of leap years the Gregorian calendar has an average length of year equal to 365.2425 days versus the Tropical year's 365.2422 days. The first day of Passover is 15 Nisan and is converted to the Gregorian Date below based on a formula by Gauss.
Purim is Pesach - 30 days and Rosh Hashana is Pesach + 163 days.
In many astronomical calculations, we need to know the number of days in the year up to a particular date. We shall choose our starting point as 0 hours on 0 January, equivalent to the midnight between 30 and 31 December of the previous year. This might seem to be a peculiar choice, but you will see that it simplifies our calculations so is a good one to make. Midday on 3 January can then be expressed as January 3.5 since precisely three and a half days have elapsed since January 0.0.
It is sometimes necessary to express an instant of observation as so many days and a fraction of a day after a given fundamental epoch. Astronomers have chosen this fundamental epoch as the Greenwich mean noon of 1 January 4713 BCE, that is midday as measured on the Greenwich meridian on 1 January of that year. The number of days that have elapsed since that time is referred to as the Julian day number, or Julian date. For astronomical purposes, we want to count the years logically without the one year gap introduced with 1 BCE & 1 CE. Thus the year immediately preceding 1 CE is designated 0; the other years BCE are denoted by negative numbers, each of which has an absolute value which is one less than the BCE value. Thus 10 BCE corresponds to the astronomical year -9, and 4713 BCE corresponds to -4712.
The calculator below uses the local date/time you input and first converts it to UTC, that is the time at the Greenwich meridian. This time is then converted to the Julian date. If you desire to enter time as well as the date, it must be entered as a decimal part of the day, e.g. 4.75 would be the 4th at 18:00 (or 6 pm).
It is sometimes necessary to convert a given Julian date into its counterpart in the Gregorian calendar, i.e. the calendar date at Greenwich. The method shown here works for all dates from 1 January 4713 BC.
This calculator uses the built-in functions in JavaScript to make this conversion.
Again the built-in functions in JavaScript make this conversion simple. In the entry field separate each date value by a space and each time value by a colon as shown by the placeholder.
Universal time (UT), and therefore the local civil time in any part of the world, is related to the apparent motion of the Sun around the Earth. Roughly speaking, we may take 1 solar day as the time between two successive passages of the Sun across the meridian as observed at a particular place. Astronomers are interested, however, in the motion of the stars; in particular they need to use a clock whose rate is such that any star is observed to return to the same position in the sky after exactly 24 hours have elapsed according to the clock. Such a clock is called a sidereal clock and its time, being regulated by the stars, is called sidereal time (ST). Solar time, of which UT is an example, is not the same as sidereal time because during the course of 1 solar day the Earth moves nearly 1 degree along its orbit round the Sun. Hence, the Sun appears progressively displaced against the background of stars when viewed from the Earth; turning that around, the stars appear to move with respect to the Sun. Any clock, therefore, which keeps time by the Sun does not do so by the stars.
There are about 365.25 solar days in the year, the time taken by the Sun to return to the same position with respect to the background of stars. During this period, the Earth makes about 366.25 revolutions around its own axis; there are therefore this many sidereal days in the year. Each sidereal day is thus slightly shorter than the solar day, 24 hours of sidereal time corresponding to 23h 56m 04s of solar time. Universal time and Greenwich sidereal time agree at one instant every year at the autumnal equinox (around 22 September). Thereafter, the difference between them grows in the sense that sidereal time runs faster than universal time, until exactly half a year later the difference is 12 hours. After 1 year, the times again agree. The formal definition of sidereal time is that it is the hour angle of the vernal equinox.
The following calculator is accurate to 0.1 second. If minutes and/or seconds are 0, then enter zero's between colons as needed.
Here we deal with the reverse problem of the previous section, namely that of converting a given GST into the corresponding UT. The problem is complicated, however, by the fact that the sidereal day is slightly shorter than the solar day so that on any given calendar date a small range of sidereal times occurs twice. This range is about 3m 56s long, the sidereal times corresponding to UT 0h to 0h 3m 56s occurring again from UT 23h 56m 04s to midnight. The method given here correctly converts sidereal times in the former interval, but not in the latter.
The Greenwich sidereal time discussed in the previous sections is the sidereal time correct for observations made on the Greenwich meridian, longitude 0°. It is in fact the local sidereal time (LST) for the Greenwich meridian. As you move west or east from longitude 0°, however, the local sidereal time gets earlier or later respectively because the hour angle of the vernal equinox, which defines the local sidereal time, changes. You can calculate your local sidereal time, given the Greenwich sidereal time, very easily as the difference between the two times in hours is simply the geographical longitude in degrees divided by 15. Longitudes west give local sidereal times earlier than GST, and longitudes east later. You should express longitudes E as positive numbers, and longitudes W as negative numbers.
This problem is the reverse of that treated above, namely, given the local sidereal time at a particular place, what is the corresponding Greenwich sidereal time?
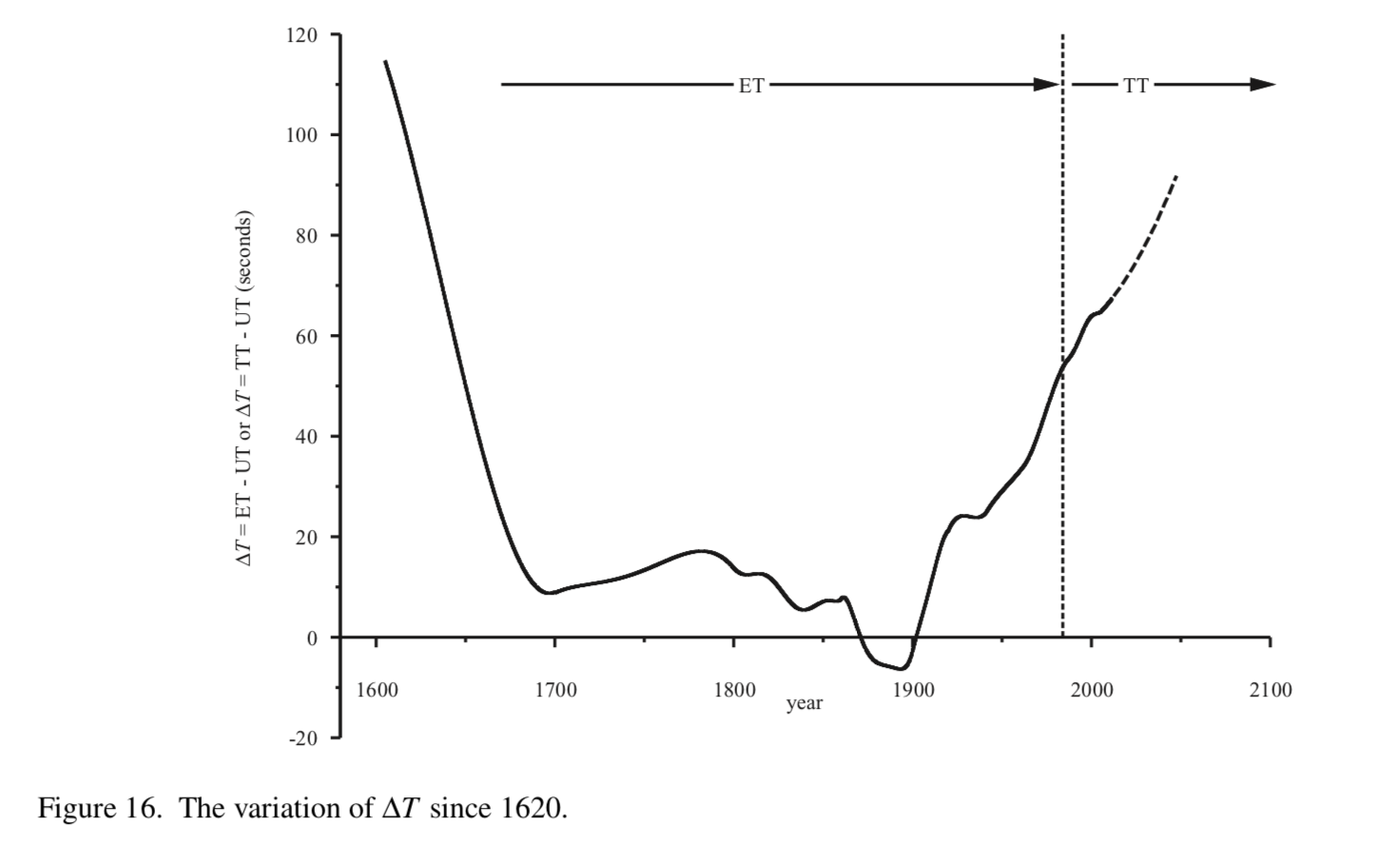
Universal and sidereal times are both tied directly to the period of the rotation of the Earth about its polar axis. The Earth is being used in effect as the balance wheel of a cosmic clock whose tick defines the length of the day. With the advent of extremely accurate atomic clocks, however, it has become apparent that the Earth's rotation is not strictly uniform but shows small erratic fluctuations which are not well understood. UT and ST, being reckoned by this irregular cosmic clock, are therefore not strictly uniform either. Astronomers need a system of time that is uniform since the theories of celestial mechanics assume that such a quantity exists. For example, two solid bodies in orbit about one another far away from any external influences should have an unchanging orbital period when measured on a regular clock. Before 1984, astronomers adopted ephemeris time (ET) for this purpose. It was calculated from the motion of the Moon and assumed to be uniform. Nowadays, atomic clocks provide the most uniform measure of time, and since 1984 terrestrial time (TT) has been used instead of ET. (In fact TT was called TDT, for terrestrial dynamic time, until renamed and slightly redefined by the International Astronomical Union in 1991.) TT is tied to the atomic time scale, TAI (see Section 9), by the equation:
The constant offset of 32.184 seconds was chosen to make TT equal to ET at the beginning of 1984. ET itself was chosen to agree as nearly as possible with the measure of universal time during the nineteenth century, and it is unlikely that TT will differ by more than a few minutes in the twenty-first. The primary unit of ET was the length of the tropical year at 1900 January 0.5 ET which contained 31,556,925.974 7 ephemeris seconds. The primary unit of TAI, and hence TT, is the SI second, defined to be the duration of 9,192,631,770 periods of the radiation corresponding to the transition between two hyperfine levels of the ground state of the caesium 133 atom. We need not be too concerned by all this since very high accuracy is not the aim of the book. In almost every case we can take ET = TT = UT without noticing the difference. Only when calculating the motion of the Moon, and predicting eclipses (Section 71), will it pay us to take account of the difference between ET/TT and UT. In January 2010 this was 66.07 seconds, UT being behind TT; that is:
Below is a graph showing the variation of ΔT since 1620.